I would discount the Deringer pistol reference, because they are always shot at very close range.
Hungry Horse
The OP's question is too vague or broad to provide a meaningful answer to. He does not specify whether he is asking about long range or close range, so the Deringer pistol is a valid reference. Probably not what he was thinking about, but then we can't read his mind--only what he wrote in his post.
Darly and
smylee grouch do point out some important variables in terms of velocities and energies as they relate to barrel length and bore volume. They are right in their intuitive thinking.
I hesitate to provide this link because the math is pretty intimidating and tends to make one's eyes glaze over, but this is some very interesting work on internal ballistics of black powder. I think the author is Henning Umland.
https://www.celnav.de/muzzleloaders/internal_ballistics.htmThis graph is Fig. 1 in the link above. The blue line represent pressure and the orange line represents mechanical work which can be equated to muzzle energy. The x-axis is bore volume from V
p, the volume of powder, to V
b, the total bore volume. In other words, the x-axis represents the bore volume from in front of the powder to the end of the barrel. This graph illustrates Daryl's point, "due to having longer to work with the expanding gasses. The powder is burned in relatively short piece of barrel, but the length of barrel determines how long those gasses have to, well, expand." Daryl is describing the principle of Boyle's law.
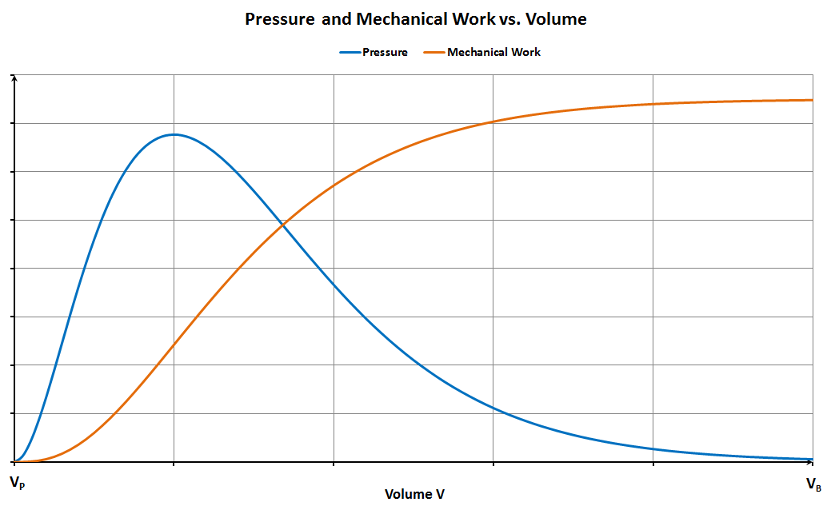
There is a point of diminishing returns on the orange curve where it starts bending over and approaches an asymptote. Longer and longer barrels increase the muzzle energy or velocity by smaller and smaller amounts.
The orange curve also illustrates the Deringer pistol and mortar situation. The orange curve is bending in the other direction at the very low volumes or barrel lengths. The projectile is accelerated by the initial combustion and expansion of the gases, but doesn't get the benefit of the additional acceleration of the gases continuing to expand in a longer barrel.
In between these two areas of curvature, the orange curve is almost a straight line where increasing volume or barrel length has a proportional impact on muzzle energy and velocity.
I would guess that this is the part of the curve the OP was most concerned about and the area most of our pistols and rifles operate in.
There are some other interesting insights in Mr. Umland work.
It takes some special equipment to measure the blue pressure curve in the graph above so he took a bunch of experimental data published in
Blackpowder Loading Manual, 3rd Edition by Sam Fadala and used the measured velocities and muzzle energy along with barrel dimensions, ball weight, and powder charge and performed some multivariate statistical analysis on it.
As a reminder, muzzle energy, E
0, is proportional to the square of the muzzle velocity, v
0.
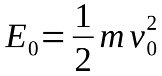
The end result is an equation (eq. 7 in the paper) relating muzzle energy, E
0, to mass or weight of powder, m
p, and mass or weight of round ball, m
b, and length of barrel, L
B. The constants "a" and "b" are derived from the regression analysis.
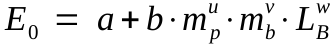
The constants thus found with 3FG powder are:
a = −92.665
b = 3.112
u = 0.738
v = 0.282
w = 0.417
Mr. Umland notes some limitations or restrictions with this approach.
Equation 7 yields an average value of the muzzle energy resulting from a given combination of powder weight (3FG), ball weight (round balls only), and bore length. The equation is only valid for powder charges in the usual range and should not be used for exotic charges, for example 100 grains of powder in combination with a .32 cal (45 grains) round ball. Further, the equation will lead to inaccurate results when used for pocket pistols with extremely short barrels since these are outside the observed range (LB = 6.0"- 41.5").
Mr. Umland's emperical equation gives results as we would expect such as shown in his Fig. 8. The muzzle energy for a given powder charge is much higher in a 24 inch rifle barrel than a 9 inch pistol barrel. Both rifle and pistol are .45 caliber.
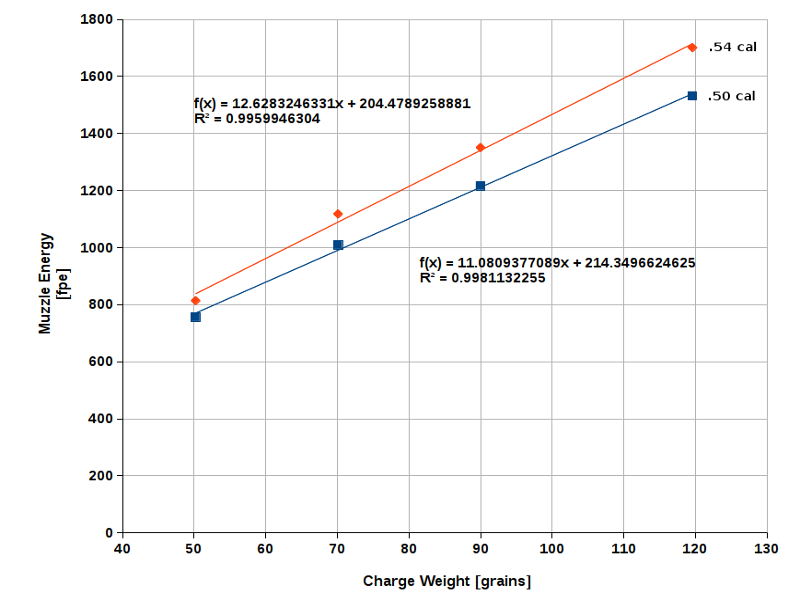
Similarly, his Fig. 9 shows a .54 caliber barrel compared to a .50 caliber barrel of the same length yields higher muzzle energy for a given powder charge. No surprise here.
One result he got that I didn't expect is his comparison of a .36 caliber barrel to a .32 caliber barrel shown in his Fig. 11.
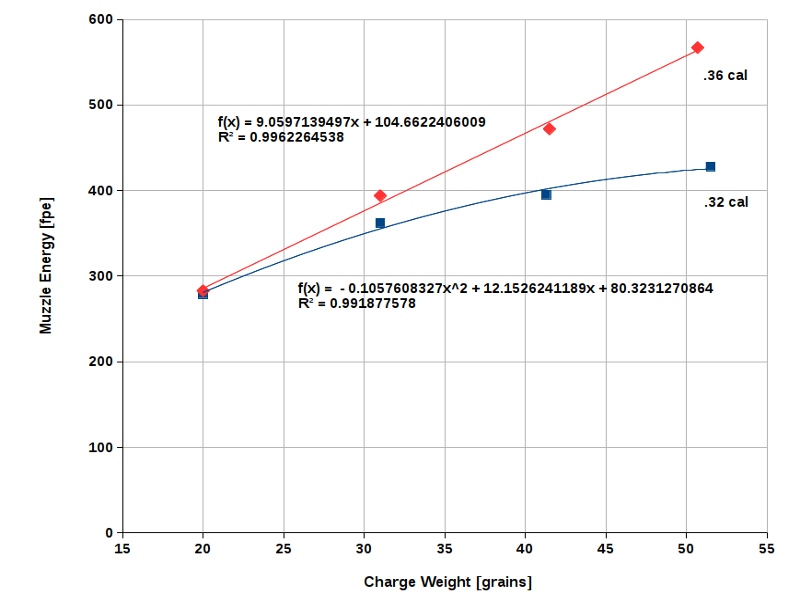
The .36 cal ball shows the same behavior as seen in Fig. 7 through Fig. 9, i. e., a more or less linear rise of E0 with increasing powder weight. As expected, the energy gained from 50 grains of powder is smaller in this case than with big-bore rifles (compare with Fig. 9). The real surprise is the behavior of the .32 cal ball. With a light powder charge (20 grains), it delivers almost the same muzzle energy as the bigger .36 cal ball. However, the curve is not linear here but flattens out rapidly as the powder weight increases (u<1). As a result, the .32 cal ball needs about 50 grains of powder to produce the same energy as a .36 cal ball with a powder charge of only 35 grains. How can we explain this? Apart from the smaller expansion ratio, the unfavorable ratio of powder weight to ball weight probably becomes a dominant factor here. Above 45 grains, the powder weight surpasses the ball weight in this case. This means that a high portion of the mechanical energy released by the powder is consumed to accelerate the inert mass of the combustion products (gases and solids) and is not available to accelerate the ball. Accordingly, energy efficiency decreases considerably. Further, the shape of the curve may also be an indication that even 3FG powder is too slow for a .32 cal round ball. In other words, the inertia of this ball is so small that the latter gets blown out of the barrel while the combustion process is still in full progress, possibly not far from the pressure maximum. Remember, a heavy powder charge takes more time to burn than a light one. There must be a reason why the old .32 cal squirrel rifles sometimes had barrels as long as 40" or even more.
These results suggest that using the faster 4FG powder or Swiss Powder #1 might be the better choice for .32 cal rifles when firing round balls.
Maybe the OP will come back and explain further what he was trying to get at with his question.

